Sometimes you have a set of items -- could be Strings, could be Numbers, could be Objects, whatever -- whose order you want to randomise. This is particularly useful for quizzes and games of chance, but comes in handy in all sorts of other applications. The easiest method I've found for doing this is to stick all the items in an Array and then shuffle it like a deck of cards. But how can we do that...?

As a simple example, we'll use the letters of the alphabet:

var letters:Array = ["A", "B", "C", "D", "E", "F", "G", "H", "I", "J", "K", "L", "M", "N", "O", "P", "Q", "R", "S", "T", "U", "V", "W", "X", "Y", "Z"];

There are different approaches we can take to actually sorting this array.

The Naive Approach

We could create a second array, and copy each element of the first into a random position in the second:

The code for that might look like this (see this Quick Tip on getting a random integer within a specific range for more details):

var letters:Array = ["A", "B", "C", "D", "E", "F", "G", "H", "I", "J", "K", "L", "M", "N", "O", "P", "Q", "R", "S", "T", "U", "V", "W", "X", "Y", "Z"];
var shuffledLetters:Array = new Array(letters.length);

var randomPos:int = 0;
for (var i:int = 0; i < letters.length; i++)
{
	randomPos = int(Math.random() * letters.length);
	shuffledLetters[randomPos] = letters[i];
}

But there's one huge problem. What if the random position picked for C is 6 as well?

Here, A gets overwritten, and will therefore not be in the shuffled array. That's not what we want, so we need to check that the slot is empty before copying the letter over, and pick a different slot if it isn't:

var letters:Array = ["A", "B", "C", "D", "E", "F", "G", "H", "I", "J", "K", "L", "M", "N", "O", "P", "Q", "R", "S", "T", "U", "V", "W", "X", "Y", "Z"];
var shuffledLetters:Array = new Array(letters.length);

var randomPos:int = 0;
for (var i:int = 0; i < letters.length; i++)
{
	randomPos = int(Math.random() * letters.length);
	while (shuffledLetters[randomPos] != null)		//repeat as long as the slot is not empty
	{
		randomPos = int(Math.random() * letters.length);	//pick a different slot
	}
	shuffledLetters[randomPos] = letters[i];
}

That works. Problem is, it's inefficient. See, the letter A is guaranteed to fit into the slot picked, because it's the first letter chosen, so all the slots will be empty. With B, there's a 25 in 26 chance that the first slot picked will be empty. When we're half-way through the alphabet, this chance drops to 50/50. By the time we reach V, there's a 50/50 chance that we won't find an empty slot until the fourth attempt.

This means we're very likely to be calling Math.random() wayyyyy more than 26 times. And Math.random() is a relatively slow function. What's another approach we can take?

The Middle-Man Approach

What if we stored a list of all the empty slots in a third array, which would shrink as we went through them?

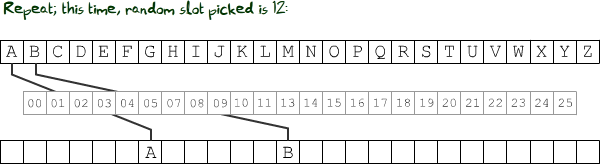
...and so on, repeating until the array of empty slots contains no elements. The code for that would look like this:

var letters:Array = ["A", "B", "C", "D", "E", "F", "G", "H", "I", "J", "K", "L", "M", "N", "O", "P", "Q", "R", "S", "T", "U", "V", "W", "X", "Y", "Z"];
var shuffledLetters:Array = new Array(letters.length);

var emptySlots:Array = new Array();
for (var n:int = 0; n < letters.length; n++)
{
	emptySlots.push(n);
}

var randomPos:Number = 0;
var actualSlot:Number = 0;
for (var i:int = 0; i < letters.length; i++)
{
	randomPos = int(Math.random() * emptySlots.length);		//note emptySlots.length not letters.length
	actualSlot = emptySlots[randomPos];
	shuffledLetters[actualSlot] = letters[i];
	emptySlots.splice(randomPos, 1);
}

Here we use the Array.splice() method to remove a single element from the list of empty slots. This actually removes the element, rather than just setting its value to null; so, after splicing the first slot, emptySlots.length will be 25 rather than 26.

This splice() function is great; we can use it for a third approach to shuffling that cuts out this middle man array.

The Splicing Approach

Instead of removing elements from the array of empty slots when we're done with them, we could remove them from the original, unshuffled array.

This doesn't sound very useful at first -- but what if we picked elements from the original array at random, instead of picking their destinations at random?

...and so on, until the first array contains no elements.

Unlike the other two approaches, we end up without the original array. Whether this is a problem or not depends on this project.

The code could look like this:

var letters:Array = ["A", "B", "C", "D", "E", "F", "G", "H", "I", "J", "K", "L", "M", "N", "O", "P", "Q", "R", "S", "T", "U", "V", "W", "X", "Y", "Z"];
var shuffledLetters:Array = new Array(letters.length);

var randomPos:Number = 0;
for (var i:int = 0; i < shuffledLetters.length; i++)	//use shuffledLetters.length because splice() will change letters.length
{
	randomPos = int(Math.random() * letters.length);
	shuffledLetters[i] = letters[randomPos];	//note this the other way around to the naive approach
	letters.splice(randomPos, 1);
}

In fact, since splice() returns an Array of all the elements you are splicing, we could simplify the code a little:

var letters:Array = ["A", "B", "C", "D", "E", "F", "G", "H", "I", "J", "K", "L", "M", "N", "O", "P", "Q", "R", "S", "T", "U", "V", "W", "X", "Y", "Z"];
var shuffledLetters:Array = new Array(letters.length);

var randomPos:Number = 0;
for (var i:int = 0; i < shuffledLetters.length; i++)
{
	randomPos = int(Math.random() * letters.length);
	shuffledLetters[i] = letters.splice(randomPos, 1)[0];	//since splice() returns an Array, we have to specify that we want the first (only) element
}

That's neater. I've got one more approach to share; this one is very different to the others we've used so far.

The Sorting Approach

Arrays have a method, sort(), which by default rearranges all the elements of the array into ascending alphanumerical order, like so:

var mixedLetters:Array = ["G", "B", "P", "M", "F"];
mixedLetters.sort();
//mixedLetters is now ["B", "F", "G", "M", "P"]

You can pass options to this method, like Array.DESCENDING, which reverses the order of the sort:

var mixedLetters:Array = ["G", "B", "P", "M", "F"];
mixedLetters.sort(Array.DESCENDING);
//mixedLetters is now ["P", "M", "G", "F", "B"]

(There are other options, and you can pass as many of them as you like.)

You can also pass a reference to a function, which tells Flash how to decide which order any two items belong in. For example, this function could be used for numeric sorting:

function numericalSort(a:Number, b:Number):Number
{
	if (a < b) return -1;
	if (a == b) return 0;
	if (a > b) return 1;
}

Flash looks at each pair of adjacent items in the array, and rearranges them according to this function: it swaps them if the value 1 is returned, and leaves them alone otherwise. (Unless you pass Array.DESCENDING as well as the function, in which case it swaps them if the value -1 is returned, and leaves them alone otherwise.) Flash repeats this across the whole array over and over again until all pairs return 0 or -1 (0 or 1 if using Array.DESCENDING).

We can mess with this. Instead of giving it a genuine reason why any two elements should be swapped, we can just tell it to swap them at random, using a sort function like this:

function randomSort(a:*, b:*):Number	//* means any kind of input
{
	if (Math.random() < 0.5) return -1;
	else return 1;
}

Easy! Now we can use it in our code like so:

function randomSort(a:*, b:*):Number
{
	if (Math.random() < 0.5) return -1;
	else return 1;
}

var letters:Array = ["A", "B", "C", "D", "E", "F", "G", "H", "I", "J", "K", "L", "M", "N", "O", "P", "Q", "R", "S", "T", "U", "V", "W", "X", "Y", "Z"];
letters.sort(randomSort);

//(no need for the shuffledLetters[] Array)

Please note that the resulting array will not be as randomly shuffled as the other approaches we've used -- in this approach, there isn't an even 1/26 chance that any given letter will end up in any given slot. This is because we're only swapping adjacent pairs of elements, and doing no more than that. Still, it's a neat method :)

There are plenty of other methods, I know. Got any you like better than these?

Edit: Here's a great post with some very cool visualisations, explaining the Fisher-Yates shuffle, which works in place. I highly recommend it!