The Set is a collection type that implements the basic algebraic set algorithms including union, intersection, difference, and symmetric difference. Each of these algorithms will be explained in detail in their respective sections.
Overview
Conceptually, sets are collections of objects that often have some commonality. For example, we might have a set that contains positive even integers:
[2, 4, 6, 8, 10, ...]
And a set that contains positive odd integers:
[1, 3, 5, 7, 9, ...]
These two sets do not have any values in common. Now consider a third set that is all the factors of the number 100:
[1, 2, 4, 5, 10, 20, 25, 50, 100]
Given these sets, we can now answer the question, “Which factors of 100 are odd?” by looking at the set of odd integers and the set of factors of 100 and seeing which values exist in both sets. But we could also answer questions such as, “Which odd numbers are not factors of 100?” or, “Which positive numbers, even or odd, are not factors of 100?”
This may not seem very useful, but that’s because the example is somewhat contrived. Imagine if the sets were every employee at a company and every employee who had completed the mandatory annual training.
We could easily answer the question, “Which employees have not completed the mandatory training?”
We can continue to add additional sets and start to answer very complex questions such as, “Which full-time employees on the sales team who have been issued a corporate credit card have not attended the mandatory training on the new expense reporting process?”
Set Class
The Set class implements the IEnumerable interface and accepts a generic argument which should be an IComparable type (testing for equality is necessary for the set algorithms to function).
The members of the set will be contained in a .NET List class, but in practice, sets are often contained in tree structures such as a binary search tree. This choice of underlying container affects the complexity of the various algorithms. For example, using the List, Contains has a complexity of O(n), whereas using a tree would result in O(log n) on average.
In addition to the methods we will be implementing, the Set includes a default constructor and one that accepts an IEnumerable of items to populate the set with.
public class Set : IEnumerable
where T: IComparable
{
private readonly List _items = new List();
public Set()
{
}
public Set(IEnumerable items)
{
AddRange(items);
}
public void Add(T item);
public void AddRange(IEnumerable items);
public bool Remove(T item);
public bool Contains(T item);
public int Count
{
get;
}
public Set Union(Set other);
public Set Intersection(Set other);
public Set Difference(Set other);
public Set SymmetricDifference(Set other);
public IEnumerator GetEnumerator();
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator();
}
Insertion
Add
| Behavior | Adds the item to the set. If the item already exists in the set, an InvalidOperationException is thrown. |
| Performance | O(n) |
When implementing the Add algorithm, a decision needs to be made: will the set allow duplicate items or not? For example, given the following set:
[1, 2, 3, 4]
If the caller attempts to add the value three, will the set become:
[1, 2, 3, 3, 4]
While this might be acceptable in some contexts, it’s not the behavior we are going to implement. Imagine a set that contains all the students at a local college. It would not be logical to allow the same student to be added to the set twice. In fact, attempting to do so is likely an error (and will be treated as such in this implementation).
Note: Add uses the Contains Method
public void Add(T item)
{
if (Contains(item))
{
throw new InvalidOperationException("Item already exists in Set");
}
_items.Add(item);
}
AddRange
| Behavior | Adds multiple items to the set. If any member of the input enumerator exists in the set, or if there are duplicate items in the input enumerator, an InvalidOperationException will be thrown. |
| Performance | O(mn), where m is the number of items in the input enumeration and n is the number of items currently in the set. |
public void AddRange(IEnumerable items)
{
foreach (T item in items)
{
Add(item);
}
}
Remove
| Behavior | Removes the specified value from the set if found, returning true. If the set does not contain the specified value, false is returned. |
| Performance | O(n) |
public bool Remove(T item)
{
return _items.Remove(item);
}
Contains
| Behavior | Returns true if the set contains the specified value. Otherwise it returns false. |
| Performance | O(n) |
public bool Contains(T item)
{
return _items.Contains(item);
}
Count
| Behavior | Returns the number of items in the set or 0 if the set is empty. |
| Performance | O(1) |
public int Count
{
get
{
return _items.Count;
}
}
GetEnumerator
| Behavior | Returns an enumerator for all the items in the set. |
| Performance | O(1) to return the enumerator. Enumerating all the items has a complexity of O(n). |
public IEnumerator GetEnumerator()
{
return _items.GetEnumerator();
}
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator()
{
return _items.GetEnumerator();
}
Algorithms
Union
| Behavior | Returns a new set that is the result of the union operation of the current and input set. |
| Performance | O(mn), where m and n are the number of items in the provided and current sets, respectively. |
The union of two sets is a set that contains all of the distinct items that exist in both sets.
For example, given two sets (each represented in red):
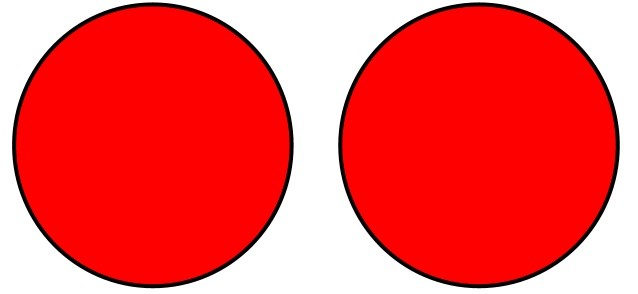
When the union operation is performed, the output set contains all of the items in both sets. If there are any items that exist in both sets, only a single copy of each item is added to the output set.
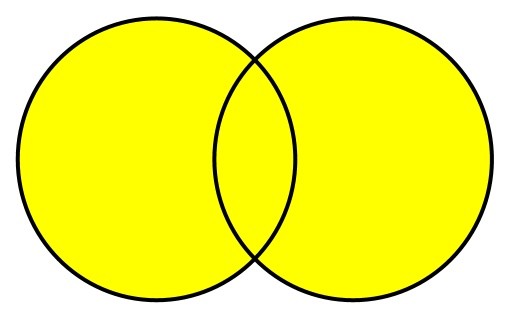
A more concrete example can be seen when we union together multiple sets of integers:
[1, 2, 3, 4] union [3, 4, 5, 6] = [1, 2, 3, 4, 5, 6]
public Set Union(Set other)
{
Set result = new Set(_items);
foreach (T item in other._items)
{
if (!Contains(item))
{
result.Add(item);
}
}
return result;
}
Intersection
| Behavior | Returns a new set that is the result of the intersection operation of the current and input sets. |
| Performance | O(mn), where m and n are the number of items in the provided and current sets, respectively. |
Intersection is the point at which two sets "intersect", for example, their common members. Using the Venn diagram from the union example, the intersection of the two sets is shown here:
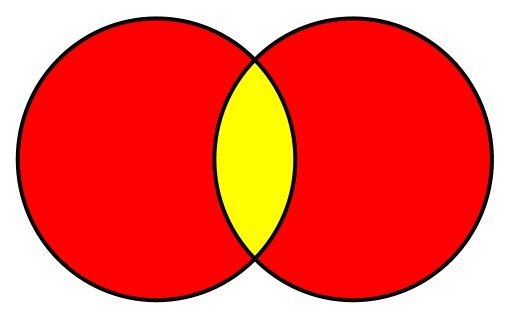
Or, using sets of integers:
[1, 2, 3, 4] intersect [3, 4, 5, 6] = [3, 4]
public Set Intersection(Set other)
{
Set result = new Set();
foreach (T item in _items)
{
if (other._items.Contains(item))
{
result.Add(item);
}
}
return result;
}
Difference
| Behavior | Returns a new set that is the result of the difference operation of the current and input sets. |
| Performance | O(mn), where m and n are the number of items in the provided and current sets, respectively. |
The difference, or set difference, between two sets is the items that exist in the first set (the set whose Difference method is being called), but do not exist in the second set (the method's parameter). The Venn diagram for this method is shown here with the returned set in yellow:
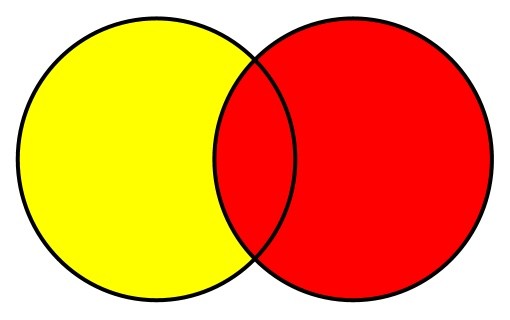
Or, using sets of integers:
[1, 2, 3, 4] difference [3, 4, 5, 6] = [1, 2]
public Set Difference(Set other)
{
Set result = new Set(_items);
foreach (T item in other._items)
{
result.Remove(item);
}
return result;
}
Symmetric Difference
| Behavior | Returns a new set that is the result of the symmetric difference operation of the current and input sets. |
| Performance | O(mn), where m and n are the number of items in the provided and current sets, respectively. |
The symmetric difference of two sets is a set whose members are those items which exist in only one or the other set. The Venn diagram for this method is shown here with the returned set in yellow
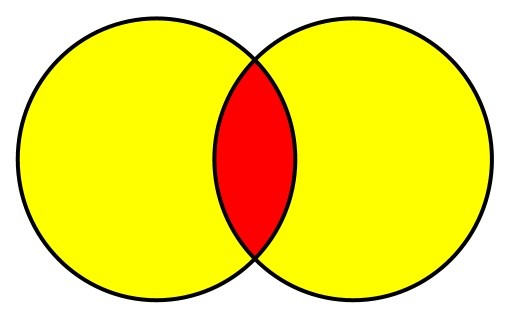
Or, using integer sets:
[1, 2, 3, 4] symmetric difference [3, 4, 5, 6] = [1, 2, 5, 6]
You may have noticed that this is the exact opposite of the intersection operation. With this in mind, let’s see what it would take to find the symmetric difference using only the set algorithms we’ve already looked at.
Let’s walk through what we want.
We want a set that contains all of the items from both sets except for those that exist in both. Or said another way, we want the union of both sets except for the intersection of both sets. We want the set difference between the union and the intersection of both sets.
Step by step, it looks like this:
[1, 2, 3, 4] union [3, 4, 5, 6] = [1, 2, 3, 4, 5, 6]
[1, 2, 3, 4] intersection [3, 4, 5, 6] = [3, 4]
[1, 2, 3, 4, 5, 6] set difference [3, 4] = [1, 2, 5, 6]
Which yields the resulting set we wanted: ([1, 2, 5, 6]).
public Set SymmetricDifference(Set other)
{
Set union = Union(other);
Set intersection = Intersection(other);
return union.Difference(intersection);
}
IsSubset
You might be wondering why I did not add an IsSubset method. This type of method is commonly used to determine if one set is entirely contained in another set. For example, we might want to know if:
[1, 2, 3] is subset [0, 1, 2, 3, 4, 5] = true
Whereas:
[1, 2, 3] is subset [0, 1, 2] = false
The reason I haven't detailed an IsSubset method is that it can be performed using existing means. For example:
[1, 2, 3] difference [0, 1, 2, 3, 4, 5] = []
An empty result set shows that the entire first set was contained in the second set, so we know the first set is a complete subset of the second. Another example, using intersection:
[1, 2, 3] intersection [0, 1, 2, 3, 4, 5] = [1, 2, 3]
If the output set has the same number of elements as the input set, we know the input set is a subset of the second set.
In a general purpose Set class, having an IsSubset method might be useful (and could be implemented more optimally); however, I wanted to make the point that this is not necessarily a new behavior, but rather just another way of thinking about existing operations.


Comments